DFS & BFS

그래프 탐색 방법은 크게 DFS(깊이 우선 탐색)와 BFS(넓이 우선 탐색)이 있다.

 

그래프(Graph)란 Node(정점)와 Edge(간선)로 이뤄진 자료구조이며 Node(정점)들은 Edge(간선)로 이어져있다.

그래프를 탐색한다는 건 한 노드를 시작으로 간선을 통해 모든 노드들을 한번씩 방문하는 것을 의미한다.

 

1. DFS (Depth-First Search) : 일단 최대한 깊게 탐색 후 옆으로 탐색

DFS

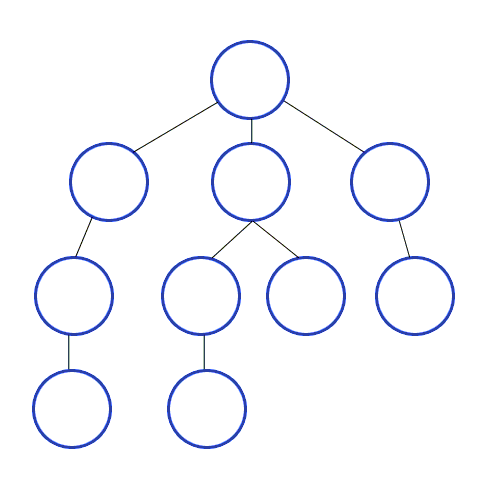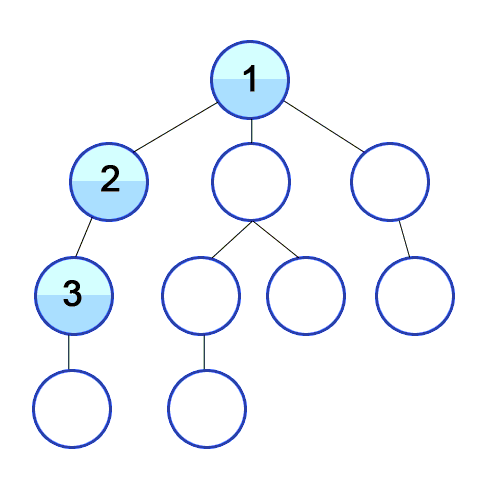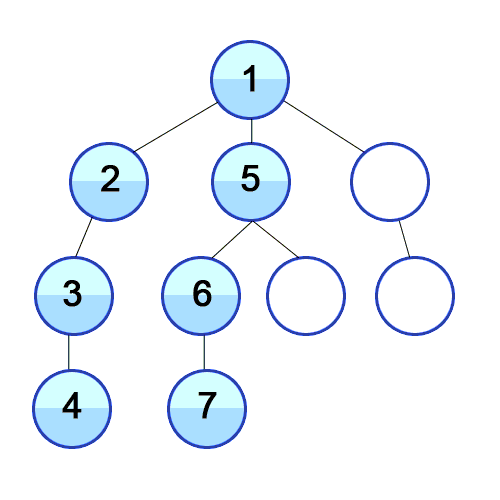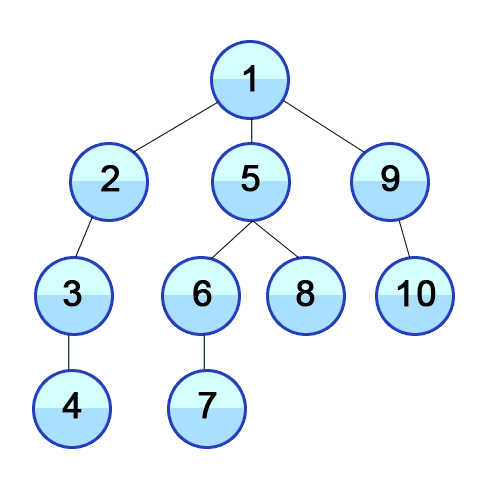
• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
  (자식들을 우선적으로 탐색하는 방법)
• 스택 또는 재귀함수로 구현 (자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다)
  
• 한 노드에서 제일 마지막 자식까지 탐색하고 돌아오는 과정을 '백트래킹(Backtracking)'
• 🔥 방문한 노드는 확실하게 확인해줘야한다. 그렇치 않으면 무한루프에 빠지게 된다.

 

DFS

 

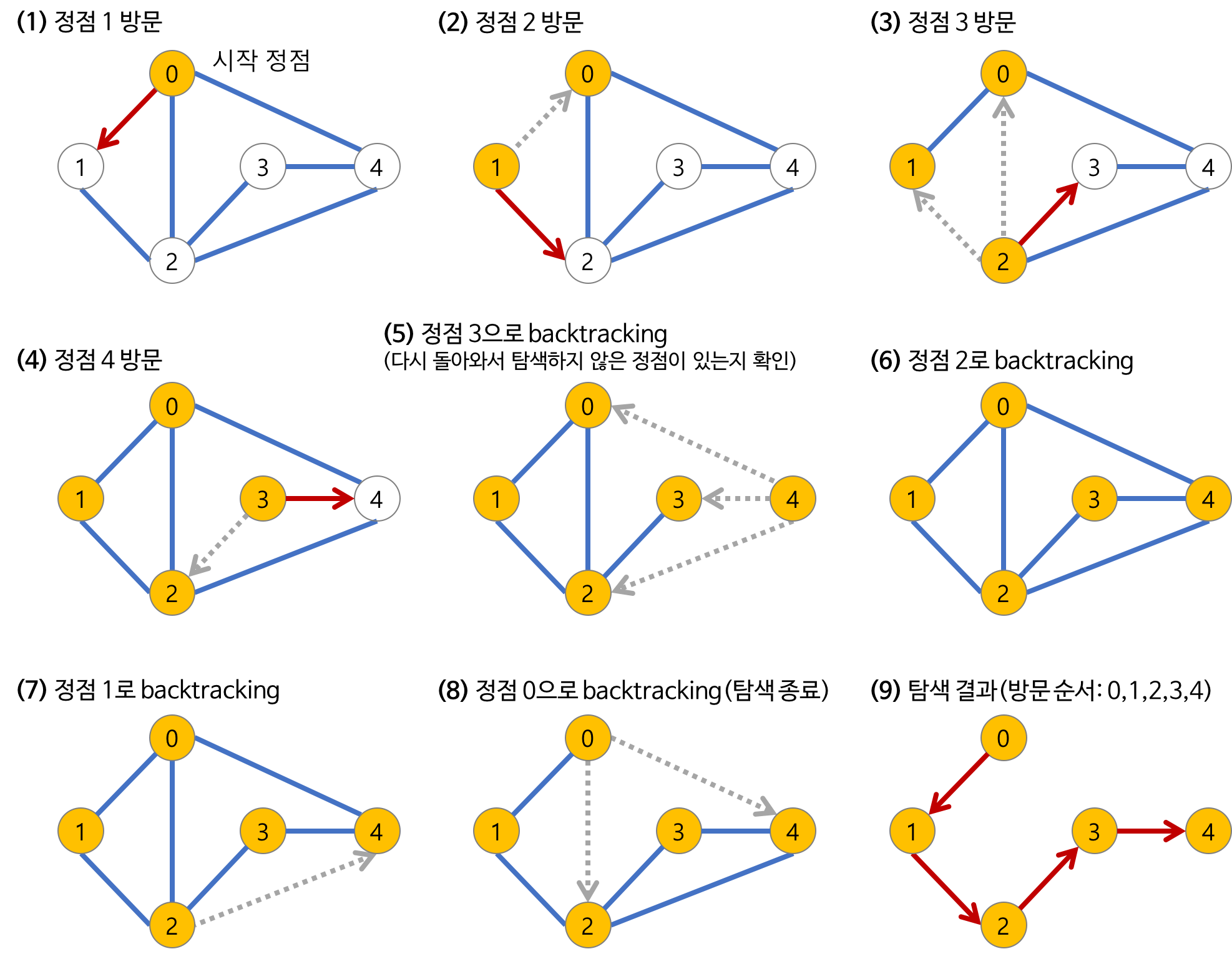
📘 순환 호출을 이용한 DFS 의사코드 (pseudocode)

void search(Node root) {
  if (root == null) return;
  // 1. root 노드 방문
  visit(root);
  root.visited = true; // 1-1. 방문한 노드를 표시
  // 2. root 노드와 인접한 정점을 모두 방문
  for each (Node n in root.adjacent) {
    if (n.visited == false) { // 4. 방문하지 않은 정점을 찾는다.
      search(n); // 3. root 노드와 인접한 정점 정점을 시작 정점으로 DFS를 시작
    }
  }
}

 

📘 순환 호출을 이용한 DFS 구현

 

import java.io.*;
import java.util.*;

/* 인접 리스트를 이용한 방향성 있는 그래프 클래스 */
class Graph {
  private int V;   // 노드의 개수
  private LinkedList<Integer> adj[]; // 인접 리스트

  /** 생성자 */
  Graph(int v) {
      V = v;
      adj = new LinkedList[v];
      for (int i=0; i<v; ++i) // 인접 리스트 초기화
          adj[i] = new LinkedList();
  }

  /** 노드를 연결 v->w */
  void addEdge(int v, int w) { adj[v].add(w); }

  /** DFS에 의해 사용되는 함수 */
  void DFSUtil(int v, boolean visited[]) {
      // 현재 노드를 방문한 것으로 표시하고 값을 출력
      visited[v] = true;
      System.out.print(v + " ");

      // 방문한 노드와 인접한 모든 노드를 가져온다.
      Iterator<Integer> i = adj[v].listIterator();
      while (i.hasNext()) {
          int n = i.next();
          // 방문하지 않은 노드면 해당 노드를 시작 노드로 다시 DFSUtil 호출
          if (!visited[n])
              DFSUtil(n, visited); // 순환 호출
      }
  }

  /** 주어진 노드를 시작 노드로 DFS 탐색 */
  void DFS(int v) {
      // 노드의 방문 여부 판단 (초깃값: false)
      boolean visited[] = new boolean[V];

      // v를 시작 노드로 DFSUtil 순환 호출
      DFSUtil(v, visited);
  }

  /** DFS 탐색 */
  void DFS() {
      // 노드의 방문 여부 판단 (초깃값: false)
      boolean visited[] = new boolean[V];

      // 비연결형 그래프의 경우, 모든 정점을 하나씩 방문
      for (int i=0; i<V; ++i) {
          if (visited[i] == false)
              DFSUtil(i, visited);
      }
  }
}

/** 사용 방법 */
public static void main(String args[]) {
    Graph g = new Graph(4);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    g.DFS(2); /* 주어진 노드를 시작 노드로 DFS 탐색 */
    g.DFS(); /* 비연결형 그래프의 경우 */
}

 

📘 DFS 시간복잡도

• DFS는 그래프(정점의 수: N, 간선의 수: E)의 모든 간선을 조회한다.
• 인접 리스트로 표현된 그래프: O(N+E)
• 인접 행렬로 표현된 그래프: O(N^2)
• 즉, 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.

 

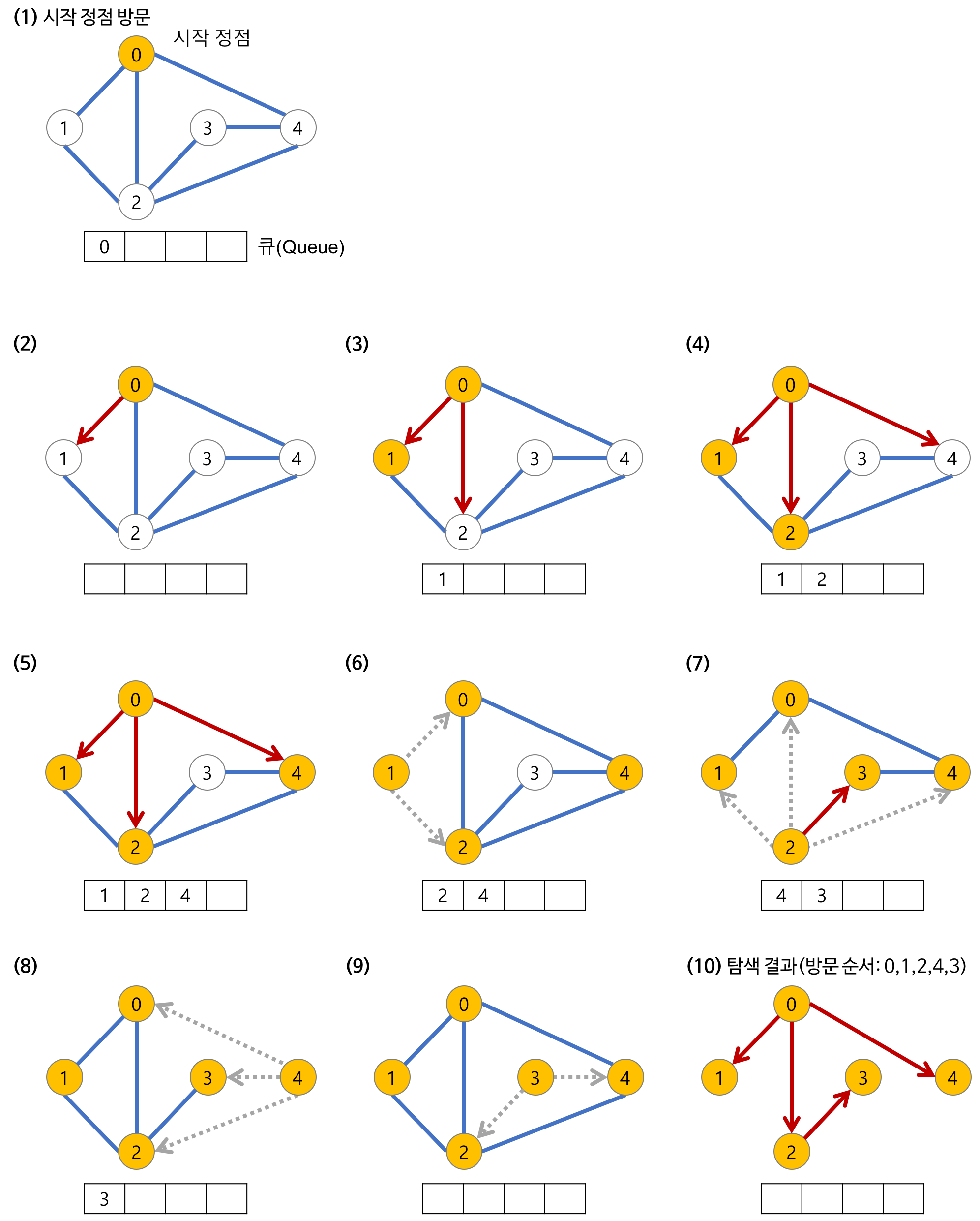
1. BFS (Breadth-First Search) : 옆에 있는 가까운 노드들부터 탐색하고 이후 깊게 탐색

BFS

 

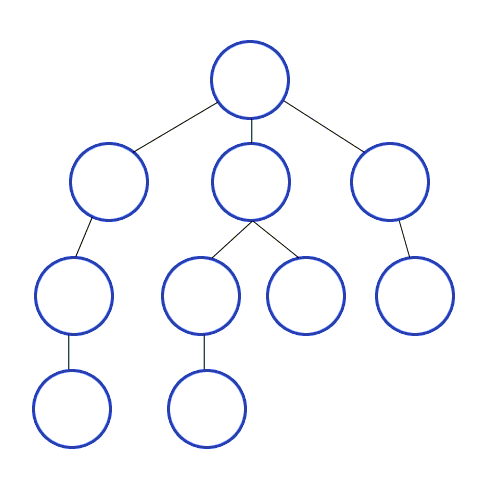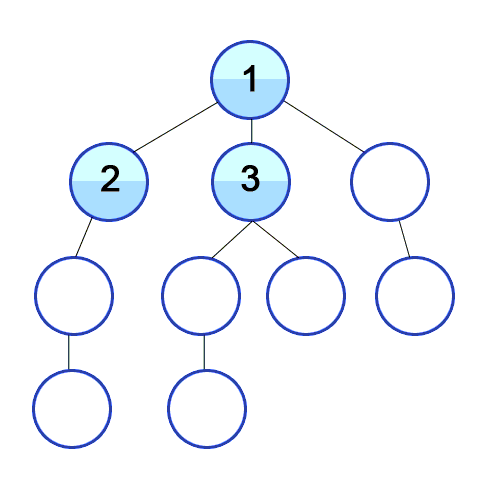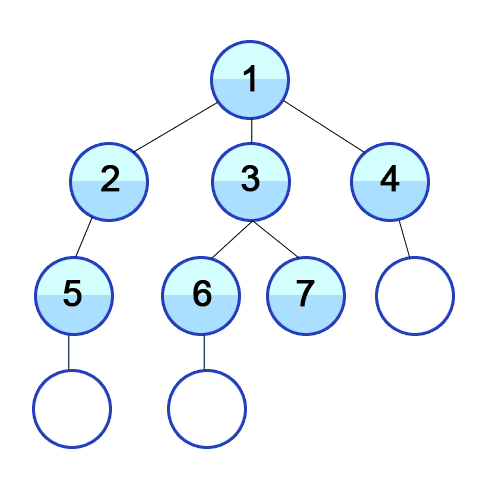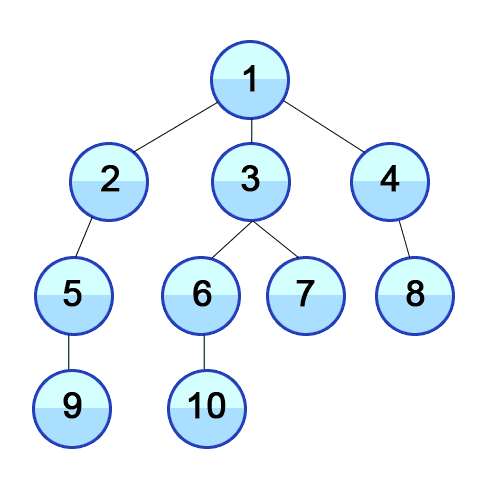
• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드부터 방문하는 방법
• 큐를 이용하여 구현
• 최단거리를 구하는 문제에서 자주 사용된다.
• 🔥 방문한 노드는 확실하게 확인해줘야한다. 그렇치 않으면 무한루프에 빠지게 된다.
  
  

BFS

📘 BFS의 의사코드 (pseudocode)

void search(Node root) {
  Queue queue = new Queue();
  root.marked = true; // (방문한 노드 체크)
  queue.enqueue(root); // 1-1. 큐의 끝에 추가

  // 3. 큐가 소진될 때까지 계속한다.
  while (!queue.isEmpty()) {
    Node r = queue.dequeue(); // 큐의 앞에서 노드 추출
    visit(r); // 2-1. 큐에서 추출한 노드 방문
    // 2-2. 큐에서 꺼낸 노드와 인접한 노드들을 모두 차례로 방문한다.
    foreach (Node n in r.adjacent) {
      if (n.marked == false) {
        n.marked = true; // (방문한 노드 체크)
        queue.enqueue(n); // 2-3. 큐의 끝에 추가
      }
    }
  }
}

 

BFS 구현

import java.io.*;
import java.util.*;

/* 인접 리스트를 이용한 방향성 있는 그래프 클래스 */
class Graph {
  private int V; // 노드의 개수
  private LinkedList<Integer> adj[]; // 인접 리스트

  /** 생성자 */
  Graph(int v) {
    V = v;
    adj = new LinkedList[v];
    for (int i=0; i<v; ++i) // 인접 리스트 초기화
      adj[i] = new LinkedList();
  }

  /** 노드를 연결 v->w */
  void addEdge(int v, int w) { adj[v].add(w); }

  /** s를 시작 노드으로 한 BFS로 탐색하면서 탐색한 노드들을 출력 */
  void BFS(int s) {
    // 노드의 방문 여부 판단 (초깃값: false)
    boolean visited[] = new boolean[V];
    // BFS 구현을 위한 큐(Queue) 생성
    LinkedList<Integer> queue = new LinkedList<Integer>();

    // 현재 노드를 방문한 것으로 표시하고 큐에 삽입(enqueue)
    visited[s] = true;
    queue.add(s);

    // 큐(Queue)가 빌 때까지 반복
    while (queue.size() != 0) {
      // 방문한 노드를 큐에서 추출(dequeue)하고 값을 출력
      s = queue.poll();
      System.out.print(s + " ");

      // 방문한 노드와 인접한 모든 노드를 가져온다.
      Iterator<Integer> i = adj[s].listIterator();
      while (i.hasNext()) {
        int n = i.next();
        // 방문하지 않은 노드면 방문한 것으로 표시하고 큐에 삽입(enqueue)
        if (!visited[n]) {
          visited[n] = true;
          queue.add(n);
        }
      }
    }
  }
}

/** 사용 방법 */
public static void main(String args[]) {
  Graph g = new Graph(4);

  g.addEdge(0, 1);
  g.addEdge(0, 2);
  g.addEdge(1, 2);
  g.addEdge(2, 0);
  g.addEdge(2, 3);
  g.addEdge(3, 3);

  g.BFS(2); /* 주어진 노드를 시작 노드로 BFS 탐색 */
}

 

📘 너비 우선 탐색(BFS) 시간 복잡도

• 인접 리스트로 표현된 그래프: O(N+E)
• 인접 행렬로 표현된 그래프: O(N^2)
• 깊이 우선 탐색(DFS)과 마찬가지로 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.

 

📒 추천 문제

📝 백준

1260 : DFS와 BFS

2178 : 미로탐색

 

---

📚 출처 

Graph

DFS vs BFS 탐색

[알고리즘] 깊이 우선 탐색(DFS)이란 - Heee's Development Blog

[알고리즘] 너비 우선 탐색(BFS)이란 - Heee's Development Blog